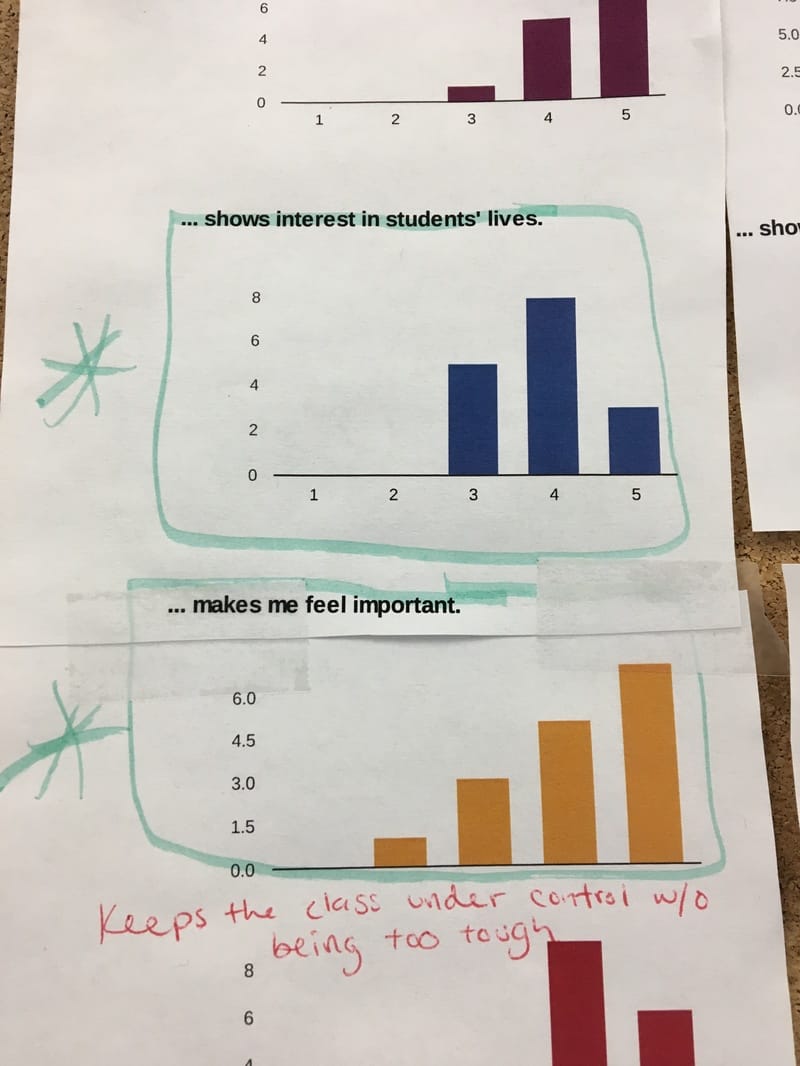
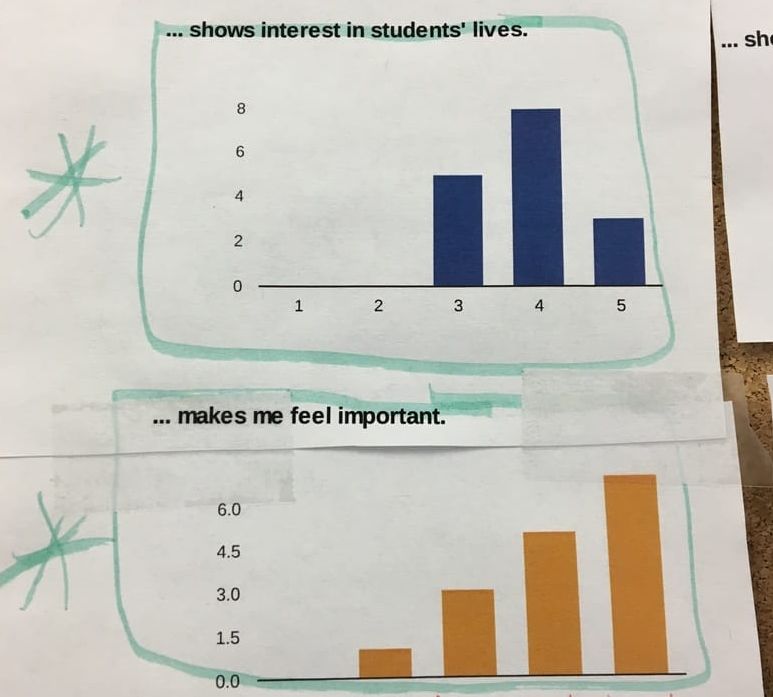
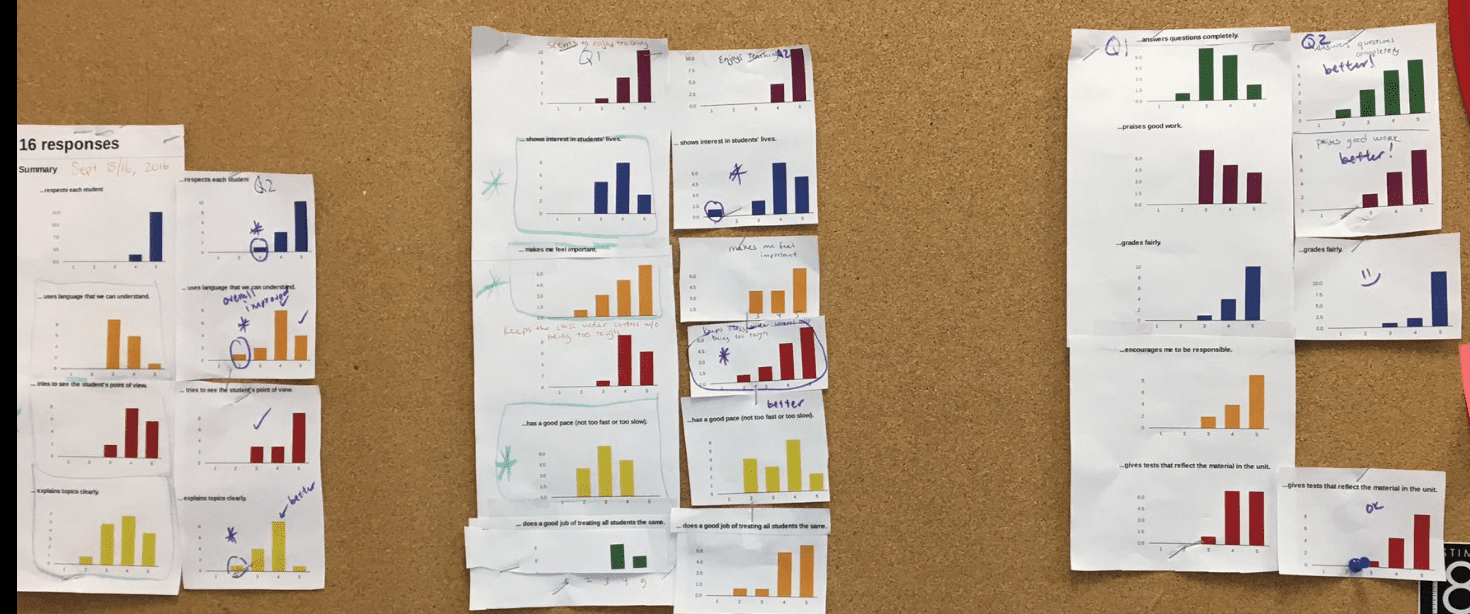
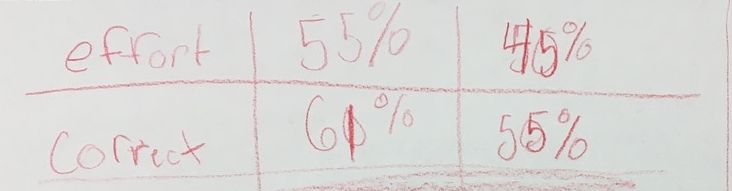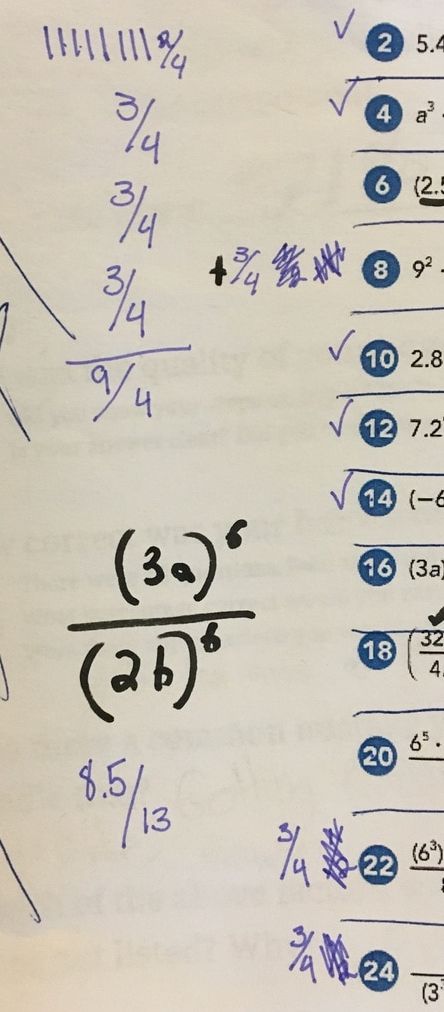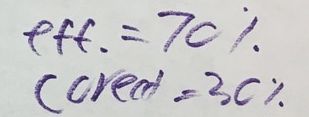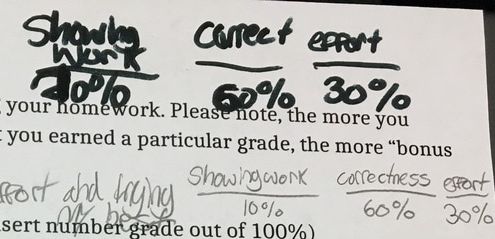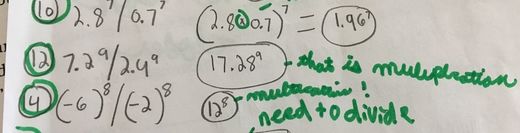|
When I first read Sara VaDerWerf's blog post on how she approaches a task she has created, #1-100, I was excited to give it a whirl with my Algebra 1 8th graders. After much thought, I decided to give Greta Bergman's approach to the same task, but with expressions to represent the numbers 1-100. The task itself on the surface screams mathy and is initially overwhelming to students. The task itself is pretty straightforward. Students pair up and together (without talking) must take turns finding and highlighting the expressions that represents the numbers 1 to 100. The catch here is that they must do it in sequential order (e.g 1, 2, 3, etc...) and they must take turns. So if partner 1 finds 1, partner 2 must then find 2.
I set a timer for 3 minutes as my students tend to have low working memory and processing speed, though in the future I may go longer. I let them find as many as they could. Most groups got to 15-20. We debriefed about their initial approach to the task and I asked what was successful, what was challenging, and how they may approach it differently the next time. Challenges they identified:
Successes:
New approaches:
New round! I reset the timer and they anxiously wanted to try the task again. This time I allowed them to think out loud. Most students improved, but not by much. On average many improved by 3-4 numbers. I asked them why they thought that was. Many identified that they were able to memorize generally where the first few numbers were. I asked how that was and they weren't quite sure. I then asked if the students thought there might be a pattern to how the numbers showed up. Many exclaimed no! this is just torture, then one students started to connect the dots, literally. She began drawing lines from 1 to 2 to 3, etc.. Her partner exclaimed that it looked like a weird connect the dot picture that kind of resembled a box or rectangle. I asked the class if we continued to find more and more numbers what would happen. They all came the the conclusion that most of the time the numbers moved from the upper left, to the upper right, to bottom right, to the bottom left then back around and around. "How might this help us?" I asked "Well, if we divide the paper into those sections we can look in each one to narrow our search!" Student 1 "Yeah! We could break the paper into quadrants!" What a great launch into vocab! "Can we try it again?!" So we did. As I mentioned before, my students tend to have lower processing speeds and working memory scores. Despite having a new approach and strategy many of my students were only able to reach 20-30 numbers. They seemed frustrated and let down. I asked them if they had an unlimited amount of time, do they think they would solve it. They all exclaimed yes. So what happened? Well, when I asked for the challenges again, my students were quick to say that although they had already solved many of the problems and COULD tell me answers when given a bit of extra time. So what did that look like during the activity? At one point, the students were searching for 16. They had zoomed into 3 to the third power. I overheard the student quickly trying to recall her facts. "3x3=9... 9x3 is.... IS IT 16?! Ms. M it's 16, right?" The students knew what three to the third power was but the actual computation of the facts escaped them. Under the pressure of the timed task they could not find strategies to answer the question themselves. "WHERE IS 25, MS. M WHERE IS IT?" Struggling because too much and the urge to finish first overwhelmed their ability to slow down and search some more. I brought these scenarios forward to the class and asked them to tell me what it meant to them. Many giggled as they themselves had the same struggles and agreed that, in the end, they knew what 9x3 was but in the moment suffered a block for how to retrieve it. So what does that look like in math class? How could this approach show it's ugly head day to day when you're doing math? Students overwhelming started sharing their fears of being wrong and weighing that against taking too long in a class. Many admitted to throwing obtuse answers out they knew were wrong in order to buy more time to think about it. Some shared the parallel anxiety of trying to fall asleep but overthinking it and then you get caught in a loop of thinking about how you cannot sleep and it prevents you from sleep. Every single kid in the room agreed that strategies went out the window when they tried to go fast or became innerly competitive about how many they could find. 'How did it feel in the moment?" I asked. "I felt frustrated that I couldn't remember the facts" "I felt lost on the paper, even though I had a smaller section to search" "I felt like I overcomplicated everything because it started to get hard and then I made it harder" "I literally forgot every math thing in my brain" I asked them how we could change our approach to the task and how this might inform how we approach math in the future. Many decided that it would be better to ask for time or take the time before rushing into problems. To continue to use the strategies they know work and when they can't immediately remember a fact, to figure it out/derive it. I told my students about the work my school has done with Jessica Minahan author of The Behavior Code and her assertion that anxiety causes IQs (particularly in the area of PS and WM) to drop significantly. Kids were looking at me like I was inside their head and knew everything about them. It was nice for students to separate out the effects of anxiety of their math performance, themselves as math learners and their ability to perform mathematics, and recognize that there are times where they will struggle. More importantly, we discussed best practices as learners when these moments do happen and how to advocate for themselves in these moments.
5 Comments
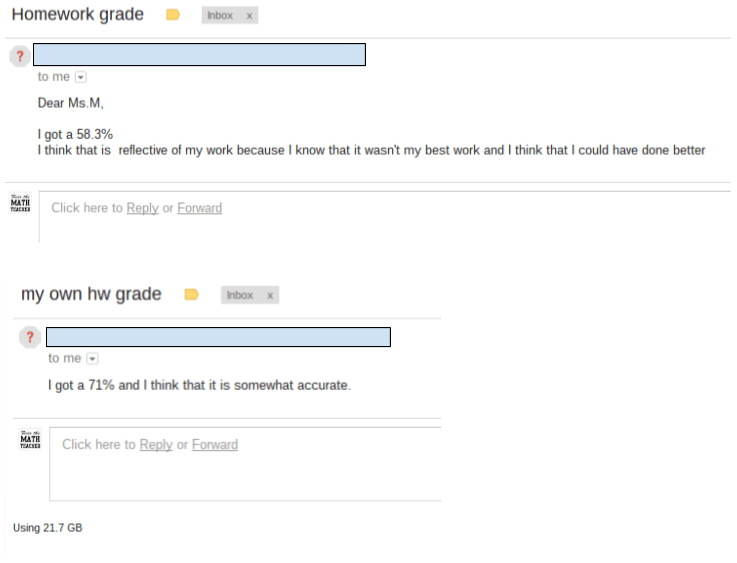
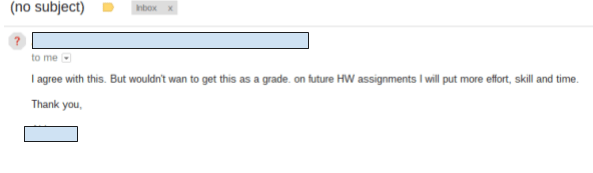
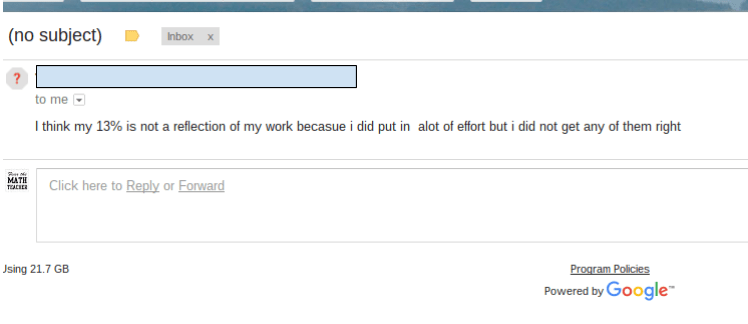
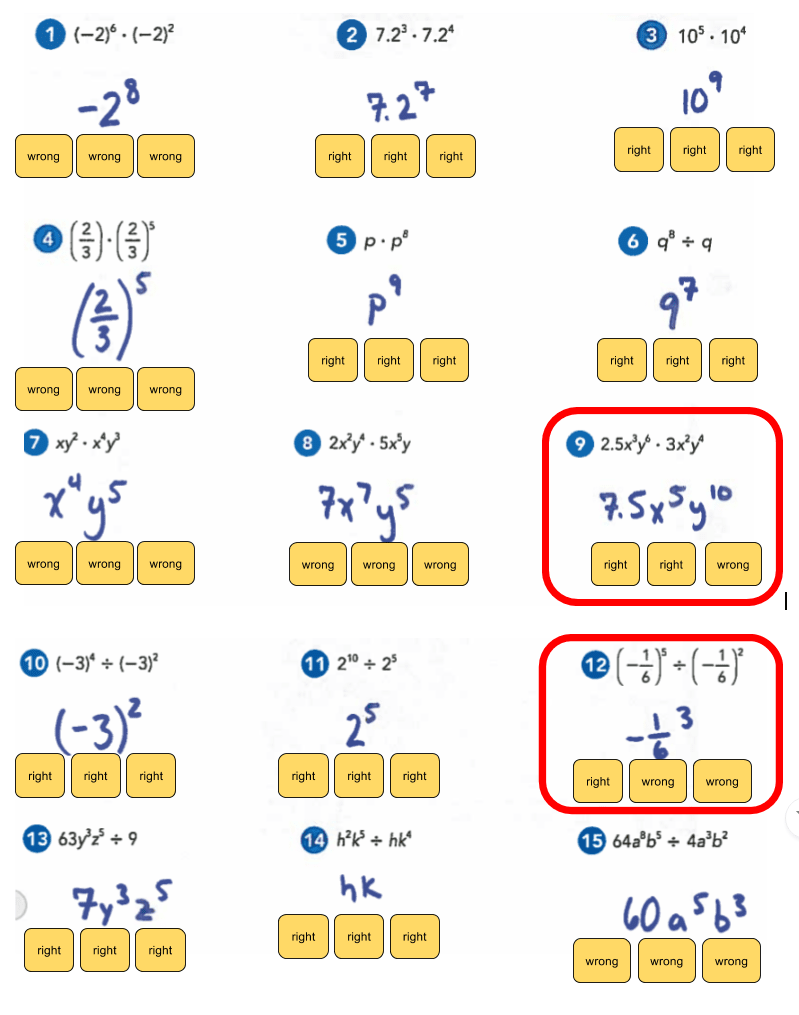
Homework irks me. I hated homework as a kid and I'm not particualrly fond of it now. I give homework for two reasons only: 1) My school requires I give it 2) Next year my students will transition to a school that gives it and I need to prepare them I hate grading homework more than I hate giving it. How do you grade homework? Do you purely go on correctness? Do you factor in how much of the assignment they complete? What if you have a slow processer, do you grade on what you deem strong effort? What if a student makes the same mistake, over and over again? Do you take off full credit? Partial? Do you take off points for not copying the problem? Not showing all their steps? AHHHHHHHHHH! A colleague of mine calls homework graded effort and classwork graded effort and work. I agree. So... I decided that I was going to have my students grade their own homework. No, I didn't want them to give me a percentage based on how many they got correct. I wanted them to develop a rubric of what they believe is important for completing homework. They also had to persaude me as to why their grade makes sense and why the values/factors they picked for their rubric matter. I handed them an answer key and away they went. Below are some guiding questions I posed to the students. I was very clear to them that these are just starting points and they did not need to include all or any of the factors listed if they did not want to. Students initially did not like the openness of this assignment. S1: What if I think effort is the most important and want it to be worth 100% of my grade Me: Make it 100% of your grade them {S1 gives me a dumbfounded look} How often do we ask students what is important to them in an assignment? I can give you that answer, almost never. We provide the rubrics and we give meaning within an assignment. For example, I hand a homework grading rubric to my students at the beginning of the year. It is quite complicated, and detailed, but essentially about 80% of the grade is based on completion of the assignment and effort (deemed on attempts toward problems and work shown to the best of their ability -- read: not all my students show their work the same way) and 20% on how correct the answers are. Is that what is important to my students? I can't grade them based on the effort they felt they put in as that's not something I can see. The 20% of the grade based on how correct the assignment was also irks me. If a student has a misconception on a rule or procedure, that misconception will carry through the entire assignment which essentially renders 20% of their grade a 0%. In these instances, I allow redos but I also consider partial credit as a student should not be faulted over and over for the same mistake due to misunderstanding. Below are some examples of the rubrics and grades within the categories that my students created: Grade I Deserve Percent of Overall Grade The student above calculated her "correctness" score by weighting each problem then taking off points. At times she gave herself partial credit if, for example, she forgot parentheses in her answer she got the majority of the points. Below is her break down of her weighted scores. On the left is her finalized point system and on the right is how it plays out on her actual homework. Another example of this is shown below: What I noticed is that students were less likely to give themselves over half credit for small mistakes than I would be. I also know that students would complain if the assignment were left in my hands and I didn't give them credit. Students really are their worst critics. Students then learned how to weight different values to calculate a total grade. Above are some examples of how kids felt they did and what their overall grades added up to. Overall, I was surprised the grades were so low. The students were incredibly hard on themselves in regard to effort. When I asked them in person after why they felt they did not deserve above a B in effort or, as for many, around a 30% for effort, many of the students told me that they never checked over their work, they didn't show any of their thinking on paper and as a result struggled to find their misconception in the problem in order to give themselves partial credit in the "correctness" category. They all felt they could spend more time on the homework. I then had students email me a sentence telling me their grade and stating whether they actually agreed with their rubric system and whether they believe their grade is an accurate reflection of their work. Students are very aware of their own effort and how they approach assignments. Many of my students were shocked by their grades, not happy with their grades, but they realized their own standards of what makes a good math assignment earned them the grade. Some students thought they deserved a B just for doing the assignment and the fact that they got 0% correct was OK because effort to them was most important. This is important for me as a teacher to realize. Not all of my students have internalized the delicate balance of correctness to effort and that is on me to dispell. Many of my students held firmly to their low grades and said they needed to do better. No amount of my grading or telling them that same message would have the same effect on them. The biggest take aways my students had on this assignment were: 1. They needed to check their work once done. Even though I tell them everyday I don't expect them to get it perfect everytime the first time and they need to check themselves. This assignment made it clear to them. 2. Students had to clearly define, for themselves, what effort means. It may not just be completing the assignment. 3. Students wanted to take more time and developed more accountability for their own work. 4. Students noticed their mistakes tended to be small mistakes rather than larger conceptual mistakes. 5. Students realized that showing their work matters when giving out partial credit (FINALLY) 6. Students developed their own understanding of what it means to weigh questions and why one might weigh some questions more than others. 7. Students realized that attempting a problem was better than skipping it if they were initially confused. 8. They recognized a pattern of their own errors while grading. By the way, this is the student who thinks he deserves a 32.5%.
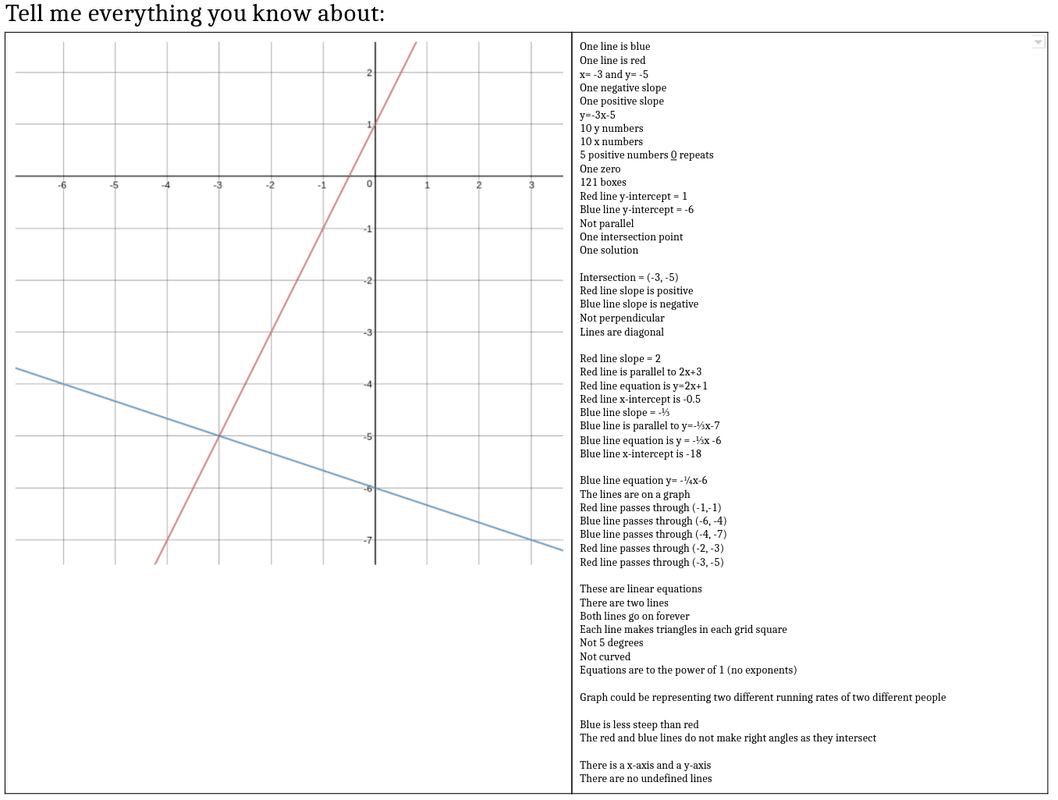
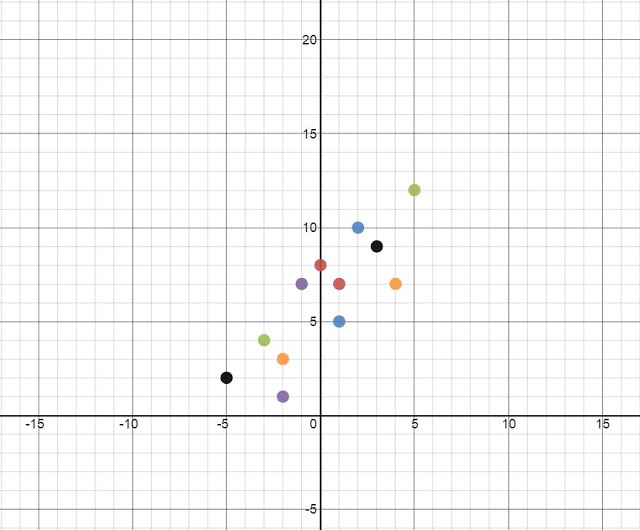
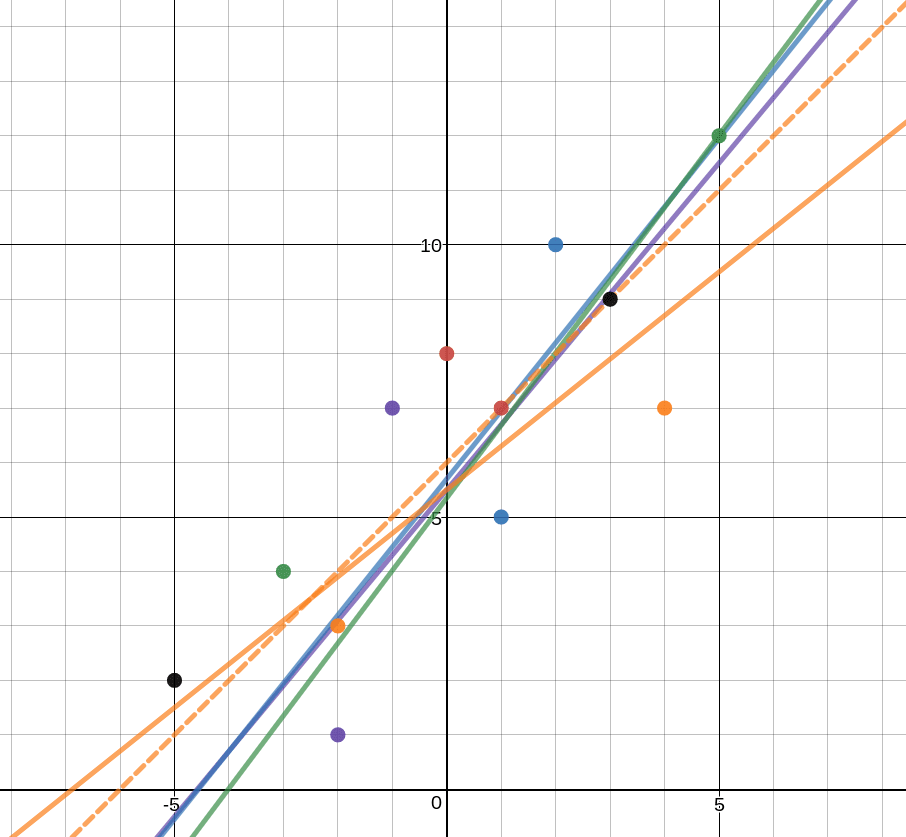
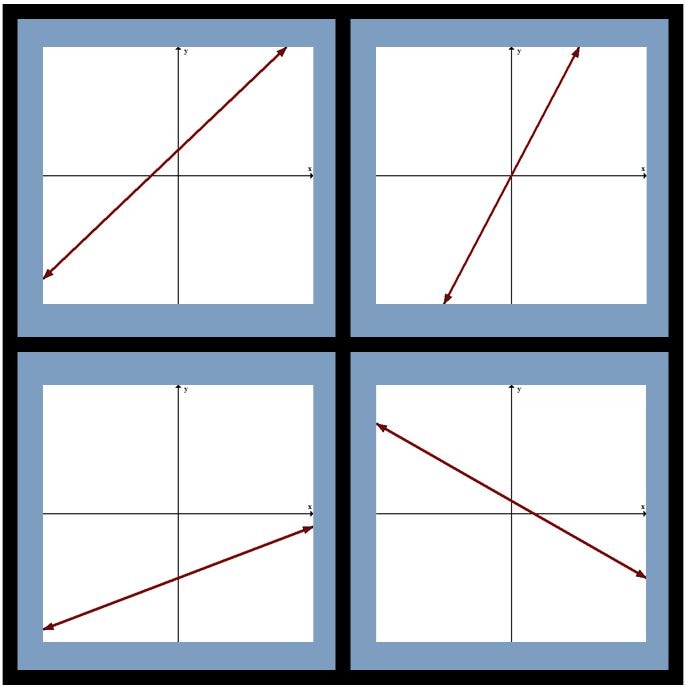
I loved this activity. I loved including the students in my grading process. For 90% of my students this had a huge impact on the way they think about and approach homework. They have a better understanding of what goes into assigning a homework grade... and honestly they are harder than I ever have been on them! I'm going to rethink this exercise so that I can get all of my students to be impacted rather than just 90%. One of my biggest fears in teaching is that despite making math real, meaningful, and easier to understand/remember my students will not remember topics from months ago. I have pretty good reason as well. I teach a population of students with Language Based Learning Difficulties (e.g. Dyslexia). My students have trouble with "math facts" (read: they can derive facts in a meaningful way given extra processing time) and they have trouble remembering steps and procedures that are NOT in isolation. No excuses however, my students are capable of thinking through math problems and using what they know to solve many problems. It's just my continual battle of fighting their old habits of memorizing without meaning... Today I took a risk. I threw up a graph of Systems of Equations on the board and I asked one question: I was thinking of a way to review prior chapters as a colleague of mine had mentioned that he recently asked his Ss to graph a line and name the equation to a line and they acted as if they had never seen it. I wanted to see where my Ss were. I wanted to engage them in an open enough way that Ss who remembered very little STILL had an entry point to the problem and they were not completely defeated by the question. For example: These are completely acceptable answers. Low entry point answers. It got them into the problem... at least they had SOMETHING on the paper and they did not know one thing. I think it is important to acknowledge these answers, especially in front of the class during discussion. They are correct answers afterall. Above is half way through our conversation about what everyone KNEW about the picture. I was both surprised and excited to see what my students remembered. There were many "Oh yeah...!" moments. There were many "I had that, too!" moments. By the end of the lesson students did a full review of linear equations and systems of equations. I even challenged some students to extend what they knew about the picture into what they may not be able to see. For example, one student decided to tell me they were not perpendicular (he proved this by using a protractor as well as telling me the slopes were not exact opposites) but also chose to tell me what the perpendicular line could be. All in all this was a good lesson for me (learning to trust that my students, when given the opportunity, will remember) and for the students using themselves as a way to remember material and extend thei knowledge through conversations. Next time I think I would have them trade with a partner and make it a bit of a competition to see who could come up with the most facts about the picture. Second half...My students have spent the past two weeks covering exponents as a precursor to our polynomial unit. Exponents can be killer for kids despite switching it up/making it more interesting by using error analysis to learn rules. Side note: my students have done an incredible job this year understanding exponent rules. They have had deep conversations about how to simplify complex exponent problems by taking small steps and they even argue about what is the "best" first move. Being their proud "Math Mom" (as I have been deemed) I decided to give my kiddos a little treat. Enter Best Fit Lines Competition courtesy of Sarah Carter at mathequalslove BAM! I threw this up on the board and told them we were going to have a competition. The goal for them is to make a best fit line for the scatterplot above. S1: What? Wait.. what's the line of best fit? Me: Great question -- what do you think a line of best fit is? S2: Maybe a line that best fits the points? S1: Like this? {starts drawing line segments to connect the dots} S2: Those are many lines, she wants JUST ONE! S3: Maybe... somewhere in the middle? Me: Intriguing... why the middle? S3: Because it would be best for all points maybe? Me: Sounds good, you have two minutes to draw your line and tell me the equation {INSERT STUDENT PANIC HERE} To my surprise no student had the same equation. Here is what we came up with: Students argued which was better without my input. Some thought the slope should generally match the slope of the points. Some thought the more points you hit with your line, the better. Some thought the ratio of points above your line to below should be about 1:1. So finally someone turned to me and asked, "So how do we determine who won?"
So we made some rules. I let them take charge. At first their "point system" went something like this: 1 pt for every point your line hits, then add the ratio of dots above to below (they conceded the that most dots should always be the denominator since 1:1 (or 1) should be the highest score. Some kids got angry. I mean, angry. After calculating the total points based on their system they groaned, "Well I could have done better if I thought the goal was to hit the most points on the scatterplot!" So, I asked them if they would like to revisit their point system. I asked the essential question: What do you think is most important when making a line that satisfies all the data? We aren't done yet but our conversation is heading toward equal number of data points above and below a line and equidistant away from the line above and below (since it needed to be the "middle" of the data). Recognition of the day? Let students take the wheel sometimes. Be purposeful in your goals and guidance within the discussion but more oftne than not, when given the opportunity, students will make sense of the math around them and it will be more meaningful when they are part of the struggle. This winter break I took my dad shopping. He and I found ourselves in Best Buy in the middle of our trip with two computers in our hands. We ended up purchasing the same computer, a cheap Lenovo IdeaPad that came with Windows10 and 1 year free of Microsoft365 all for a whopping $149. What a steal. Upon arriving home my dad and I both anxiously opened our new laptops to set them up. Until this point, everything was the same with my father and I. We both wanted a computer, we both had similar needs for the computer, and we both couldn't wait to open them. There was one difference after opening the boxes to our computer however... My father immediately reached for the manual (of which there was none) and proclaimed he needed this:  ...as he claimed he had never used Windows10 before and had to read up about it before he turned the computer on. I was a bit taken back (though I understood this is how many people live their lives) as I had already opened the computer, turned it on, and typed in my microsoft log in. I tend to do everything my trial and error. Most of the time it works out for me and I have a better understanding of whatever I am using. I am the classis, "Oh... what does this button do?" in a new car girl. That's how I learned to code and how I taught myself math concepts in 5th grade when my glorious teacher placed the "advanced" kids in the loft to read the chapter and "figure it out." It definitely takes me longer to grasp a concept, but I not only had a greater appreciation for the tasks I had a better and deeper understanding of what I had to do (especially when something went wrong). I sat there over winter break analyzing my dad's comment in relation to my teaching. My dad wanted the straightforward, easiest way, to work on his computer. Someone out there figured out Windows10 and would tell him how to best (most efficiently?) use it. They would show him the tricks and shortcuts right away so he wouldn't waste any time. That's definitely how my father operates. I find it's how many of the students I teach come into my class. They are used to their teachers handing over the fastest method to getting an answer and then are asked to apply it. Many times the first few problems in the text are exactly like the method they have seen and then the rest have changed and the students are expected to apply "what they know" (read: what you have told them) to a novel problem. Here's the thing, I teach students with language based learning difficulties. They struggle as soon as the format of a problem changes because they are overworking their working memory just to remember the procedure you told them. 49 + 15 is not 49 to all of my students + 15 The thing with shortcuts and tricks is that you are teaching children what may be the most efficient way of figuring out a problem. What we as teachers don't recognize is that it is not always the most efficient for every one of our students, nor is it efficient if a student does not UNDERSTAND it. My students often come to me confused because I spend the first few days removing myself from being an answer key to promoting #mathfights in order for the students to start reasoning themselves. Children look to teachers for validation in their answers because we have taught them to listen, do, hand in to be corrected, and then "reason" as to where they had a misstep in the problem. As a result my students don't see the point in checking their work or even questioning their approach or answer. They have told me on many occasions that their teachers before have told them it is important to check their work because they won't be able to tell them on tests whether it is correct. Seriously? So I staged an intervention this year. As a regular class warm-up I have introduced the following tasks (I will break down how I use WODB and Math mistakes briefly below and link to other blogs that write about them): 1. Which One Doesn't Belong 2. Math Mistakes/My Favorite No (error analysis) 3. Agree or Disagree 4. Flip the question/Make the Mistakes 5. Visual Patterns **sometimes Would You Rather 1. Which one doesn't belong |
Jen McAleerMS Math Department Head located in Massachusetts. I mainly work with LBDB students teaching them meaningful mathematical procedures through context. I also look to open students' eyes to the mathematical world around them Archives
January 2017
Categories |
Proudly powered by Weebly