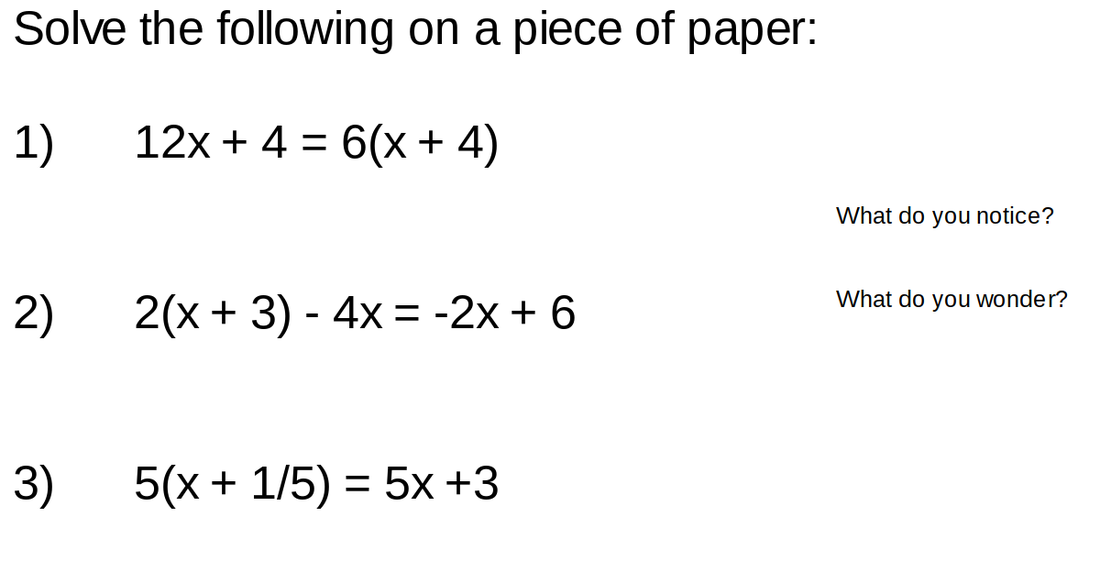|
My students often don’t know how to struggle. They don’t know how to deal and are uncomfortable with the unknown. They lack an entry point to problems or information that is new. They are solely dependent on the adult to be the answer key.
|
|
|
Enter Twitter. I had originally joined Twitter in 2014 because I wanted to follow the #SochiProblems on the feed. I left for a year and re-entered the twitterverse when my mother became sick and was in the hospital for 1-2 months. I began searching up the math blogs I had been following (Dan Meyer, Andrew Stadel, Fawn Nguyen, Jon Orr, Kyle Pearce, and Jon Stevens) on Twitter and my eyes lit up. RESOURCES! So many resources. Then came MTBOS. MTBOS introduced me to more and more math folk teaching the same topics as I was. It was then that the LS math department head and I decided to make our way to NCTM 2016 in SF. We went, listened to, and met many of the people I had been following. It was a fantastic way to renew passion for teaching math and a belief in the type of problem solving I had grown to love. A type the answers many of the questions I went to bed thinking about every night.
As I listened and read on twitter I began to develop a sequence in my head for my kids. I began to develop a daily routine that all kids should be doing. As Andrew Stadel mentioned at NCTM 2016 about classroom time we need to redesign our classroom clock. It dawned on me... I needed to make reasoning a routine in my classroom. The students needed it. My whole school needed it. I returned back from NCTM with 20 more followers on Twitter than before and a renewed passion to develop a reasoning routine and to rehash some of my lessons to make students thinking visible… not just to me but to them.. And more importantly to many their reasoning and learning valuable.
I posted many of my routines and lessons. From the Barbie Zipline, to double clotheslines, Desmos activities, WODB, Would You Rather, Open Middle, 3 act tasks, Estimation180, visualpatterns, agree or disagree conversations, sometimes, always or never tasks, number talks and notice/wonder activities. I posted my versions of them as well as what my students did with them and their reactions. I posted students out of their seats. I read Twitter posts about similar things and constantly modified my lessons based on the responses I received and how I saw other teachers teaching similar tasks. Twitter is the biggest #ObserveMe challenge ever. We teachers post resources and blog posts about lessons because we are so excited that our students are engaged but we are observing each other in the classroom as we read those blogs and respond. We are analyzing our own teaching styles as we prepare to post a picture to show our newest activity.
Double clothesline progression. Student led. I was the photographer. Fantastic conversations @JudyLarsen3 pic.twitter.com/vkrROHwCTf
— Jen McAleer (@jennifuhs4) June 9, 2016
Ziplines part 2 @classroomchef @mr_stadel pic.twitter.com/Vcx9cbzQnT
— Jen McAleer (@jennifuhs4) May 20, 2016
Agree or disagree transformations. Vertical white boards #mathfight! pic.twitter.com/qxlrOe0p9V
— Jen McAleer (@jennifuhs4) May 3, 2016
I found myself not wanting to post certain pictures and then I realized, if I didn’t want to post it… why was I teaching it that way? If my experience was that it wasn’t as meaningful as I first thought, at least meaningful enough to post to Twitter in less than 140 characters, was it not meaningful to my students? How could I improve. It sounds silly but the sheer idea that I was posting something for the potential math world to see made me a more reflective teacher ahead of time about my lessons. It made me think about how my kids would perceive and take on the lessons.
I am proud to say that my school has adopted routines around reasoning, daily. We have created powerpoints to include all the types of tasks listed above as well as intro and outro 3-act tasks for EVERY UNIT. It is not rigid. Teachers do not have to go in order. It is amazing and it is a routine. My students now ask for the warm-ups and look for connections in the material we learn. They are constantly using the terminology “I notice…” and “I wonder…”
The other day in my Algebra 1 class I threw up three equations for them to solve (see below)
I am proud to say that my school has adopted routines around reasoning, daily. We have created powerpoints to include all the types of tasks listed above as well as intro and outro 3-act tasks for EVERY UNIT. It is not rigid. Teachers do not have to go in order. It is amazing and it is a routine. My students now ask for the warm-ups and look for connections in the material we learn. They are constantly using the terminology “I notice…” and “I wonder…”
The other day in my Algebra 1 class I threw up three equations for them to solve (see below)
We had not discussed the number of solutions yet. They had only done problems with one solution. I fully expected them to be confused… to yell at me that they can’t do it or that they must have made a mistake. No. Instead most (not all, but almost!) had “I notice that the Xs went away and I wonder what that means” or “I notice that more sides of the equation are the same, which means everything would eliminate and I wonder why?” Hooked. I then explained the lesson and it was THE BEST lesson (albeit 5 minutes) I had ever taught around number of solutions. I then challenged the students to look at but not solve and identify the number of solutions by just looking (see below). They loved it.
Twitter taught me to be reflective before and after a lesson. It has taught me many ways to teach topics. It is the best resource available to math teachers. Twitter has renewed my faith in teachers, as a whole, and the love and care we have for teaching our students to not only be math students but life-long learners and to develop a passion within them for math. It starts with us. The passion flows out of Twitter for teaching and it’s contagious. I have challenged all my teachers to join Twitter. Many have and some are resistant. I think the math education world would be a far better place if we opened our minds and collaborated more on Twitter!
Finally… I leave you with the question that the Twitter verse and all it’s wonderful math minds have helped me with. So many of our students ask the question “Why are we learning…{insert any mathematical topic here}…?” Let’s start answering it.
