|
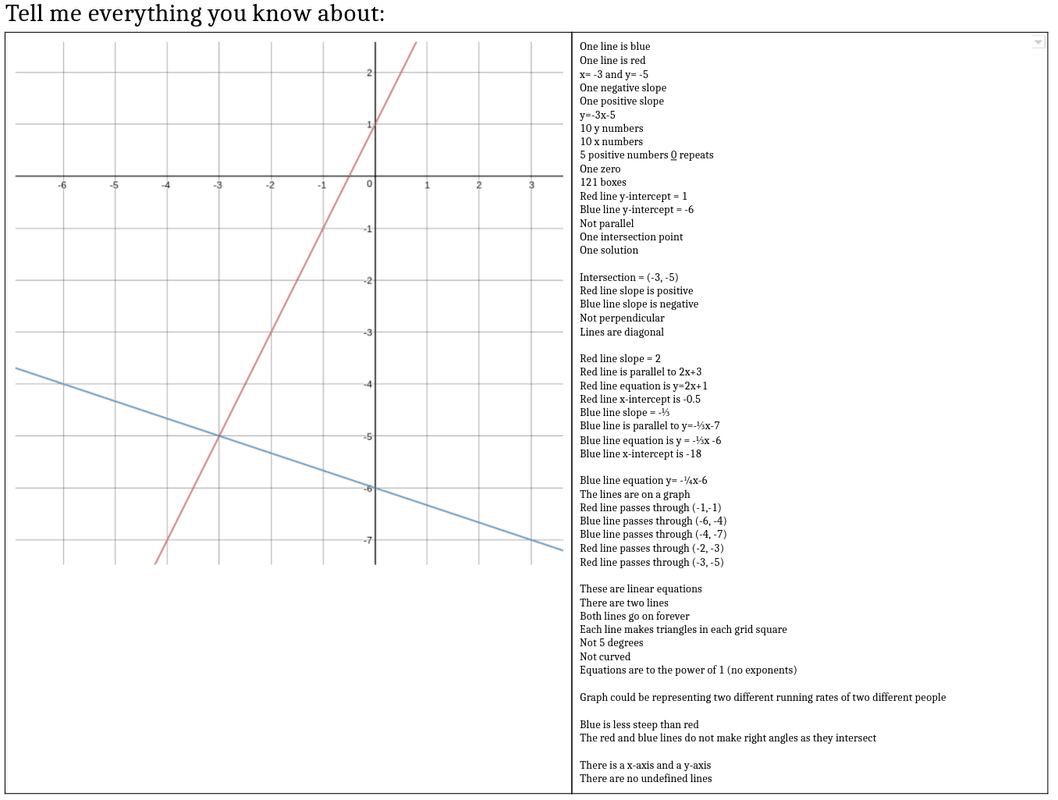
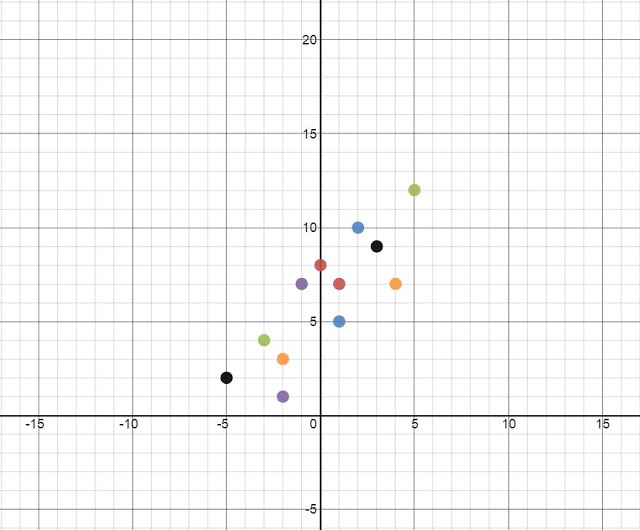
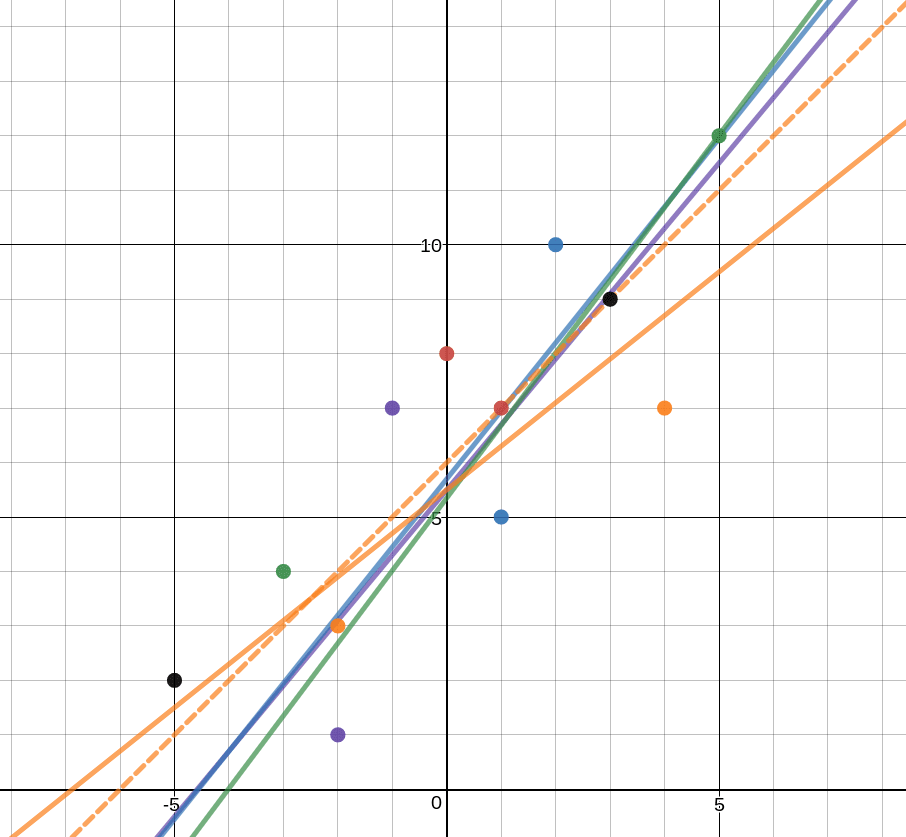
One of my biggest fears in teaching is that despite making math real, meaningful, and easier to understand/remember my students will not remember topics from months ago. I have pretty good reason as well. I teach a population of students with Language Based Learning Difficulties (e.g. Dyslexia). My students have trouble with "math facts" (read: they can derive facts in a meaningful way given extra processing time) and they have trouble remembering steps and procedures that are NOT in isolation. No excuses however, my students are capable of thinking through math problems and using what they know to solve many problems. It's just my continual battle of fighting their old habits of memorizing without meaning... Today I took a risk. I threw up a graph of Systems of Equations on the board and I asked one question: I was thinking of a way to review prior chapters as a colleague of mine had mentioned that he recently asked his Ss to graph a line and name the equation to a line and they acted as if they had never seen it. I wanted to see where my Ss were. I wanted to engage them in an open enough way that Ss who remembered very little STILL had an entry point to the problem and they were not completely defeated by the question. For example: These are completely acceptable answers. Low entry point answers. It got them into the problem... at least they had SOMETHING on the paper and they did not know one thing. I think it is important to acknowledge these answers, especially in front of the class during discussion. They are correct answers afterall. Above is half way through our conversation about what everyone KNEW about the picture. I was both surprised and excited to see what my students remembered. There were many "Oh yeah...!" moments. There were many "I had that, too!" moments. By the end of the lesson students did a full review of linear equations and systems of equations. I even challenged some students to extend what they knew about the picture into what they may not be able to see. For example, one student decided to tell me they were not perpendicular (he proved this by using a protractor as well as telling me the slopes were not exact opposites) but also chose to tell me what the perpendicular line could be. All in all this was a good lesson for me (learning to trust that my students, when given the opportunity, will remember) and for the students using themselves as a way to remember material and extend thei knowledge through conversations. Next time I think I would have them trade with a partner and make it a bit of a competition to see who could come up with the most facts about the picture. Second half...My students have spent the past two weeks covering exponents as a precursor to our polynomial unit. Exponents can be killer for kids despite switching it up/making it more interesting by using error analysis to learn rules. Side note: my students have done an incredible job this year understanding exponent rules. They have had deep conversations about how to simplify complex exponent problems by taking small steps and they even argue about what is the "best" first move. Being their proud "Math Mom" (as I have been deemed) I decided to give my kiddos a little treat. Enter Best Fit Lines Competition courtesy of Sarah Carter at mathequalslove BAM! I threw this up on the board and told them we were going to have a competition. The goal for them is to make a best fit line for the scatterplot above. S1: What? Wait.. what's the line of best fit? Me: Great question -- what do you think a line of best fit is? S2: Maybe a line that best fits the points? S1: Like this? {starts drawing line segments to connect the dots} S2: Those are many lines, she wants JUST ONE! S3: Maybe... somewhere in the middle? Me: Intriguing... why the middle? S3: Because it would be best for all points maybe? Me: Sounds good, you have two minutes to draw your line and tell me the equation {INSERT STUDENT PANIC HERE} To my surprise no student had the same equation. Here is what we came up with: Students argued which was better without my input. Some thought the slope should generally match the slope of the points. Some thought the more points you hit with your line, the better. Some thought the ratio of points above your line to below should be about 1:1. So finally someone turned to me and asked, "So how do we determine who won?"
So we made some rules. I let them take charge. At first their "point system" went something like this: 1 pt for every point your line hits, then add the ratio of dots above to below (they conceded the that most dots should always be the denominator since 1:1 (or 1) should be the highest score. Some kids got angry. I mean, angry. After calculating the total points based on their system they groaned, "Well I could have done better if I thought the goal was to hit the most points on the scatterplot!" So, I asked them if they would like to revisit their point system. I asked the essential question: What do you think is most important when making a line that satisfies all the data? We aren't done yet but our conversation is heading toward equal number of data points above and below a line and equidistant away from the line above and below (since it needed to be the "middle" of the data). Recognition of the day? Let students take the wheel sometimes. Be purposeful in your goals and guidance within the discussion but more oftne than not, when given the opportunity, students will make sense of the math around them and it will be more meaningful when they are part of the struggle.
0 Comments
Leave a Reply. |
Jen McAleerMS Math Department Head located in Massachusetts. I mainly work with LBDB students teaching them meaningful mathematical procedures through context. I also look to open students' eyes to the mathematical world around them Archives
January 2017
Categories |
Proudly powered by Weebly